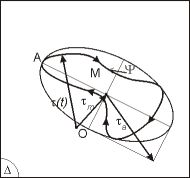
MCEM concept

Some authors have the feeling, that the minimum circle circumscribed to a shear load path is a construct in some way corresponding to the total load exerted on the shear mode crack initiation. It nevertheless have its weak point, that the equivalent shear stress amplitude can be the same for a line path as well as for a circular path. The minimum circumscribed ellipse should differ in those two examples.

There are different ways how to derive the minimum circumscribed ellipse, but the proposal of Zouain et al. in [ZAC06] seems to be the most rigorous one. Zouain et al. propose to define the minimum by minimization of the ellipse's Frobenius norm (i.e. the product of the two semi-axes). They document the variational formulation of the task and propose the complete algorithm in that paper. The implementation in PragTic is derived from this document.

The method is iterative, i.e. not exact. The breakpoints limiting the iteration process are currently set hard and users cannot influence them.

The shear stress amplitude is currently defined as the Frobenius norm itself so that the amplitude retrieval would be the same for MCEM and MCCM for the line load path. No other option have been tested up to now.

Note: There are still load paths, where the implementation of the algorithm in PragTic fails to converge. If you encounter such a case, you will be warned about it. I am not sure in this moment, if this is some singular point in the algorithm or is something bad with the algorithm itself. Any your help with this problem would be appreciated.

The algorithm can be run through the commands Tools->Loads->Decompose for a local load history on a plane.

longest projection method (LPM)

longest chord method (LCM)

minimum circumscribed ellipse method (MCEM)

This help file has been generated by the freeware version of HelpNDoc